Blog

ADRIANA HERNÁNDEZ MORALES Y MIGUEL ÁNGEL PARRA ÁLVAREZ

Introducción 

Las tendencias de los planes y programas de educación básica enfatizan, el desarrollo de competencias útiles a los alumnos para: el aprendizaje permanente, el manejo de la información, el manejo de situaciones, la convivencia y la vida en sociedad, éstas competencias integran aspectos cognitivos, afectivos y sociales (SEP, 2005). Para ello se requiere que los docentes dejen de hacer uso exclusivo de métodos expositivos y rutinarios que priorizan la memorización y el enciclopedismo y en su lugar apoyen a los alumnos a construir su conocimiento a través de la promoción de aprendizajes significativos.

En este sentido es necesario advertir que los docentes deben tener ciertas competencias para la enseñanza. Para Perrenoud (2004), la competencia es una capacidad de movilizar varios recursos cognitivos para hacer frente a un tipo de situaciones (p. 11), el autor reconoce una serie de competencias para enseñar de las cuales, retomamos la que implica al aprendizaje de los alumnos (organizar y animar situaciones de aprendizaje) que a su vez, se subdivide en competencias específicas: traducir los contenidos de enseñaza en objetivos de aprendizaje, partir de los errores y obstáculos de aprendizaje que presentan los alumnos, involucrar actividades de investigación a partir de la construcción y planificación de la didáctica. En estas competencias específicas, resalta el conocimiento de los docentes sobre cómo aprenden los alumnos y la planificación de la clase haciendo uso de materiales adecuados a su nivel cognitivo.

El modelo que subyace a las propuestas actuales es el constructivismo donde se espera que el docente reflexione sobre su práctica y analice sus creencias acerca de la enseñanza y aprendizaje, permitiéndole ser mediador entre ambos, y con ello promueva aprendizajes significativos con sentido, y preste ayuda pedagógica acorde a las necesidades de sus alumnos (Díaz-Barriga, 2004).

Sin embargo, a pesar de las reformas educativas y los talleres de actualización, aún prevalecen prácticas tradicionales de enseñanza. Entre las explicaciones que se han dado a este fenómeno en relación a los docentes, se encuentran el desconocimiento y falta de aplicación de los programas actuales, falta de motivación para capacitarse y actualizarse, poco dominio de los contenidos curriculares, perfil inadecuado y resistencia al cambio por la costumbre se no planear y las comodidades implicadas en ello (SEP, 2005). Una explicación más se relaciona con las concepciones de los docentes que obstaculizan el logro de los objetivos propuestos en los programas. Por ejemplo, en matemáticas, Putnam (1992) encontró que los maestros con una visión tradicionalista adaptan los currículos novedosos y los libros de texto a su propio estilo de enseñanza, sin que por ello se vean cambios en la práctica educativa.

Si bien es cierto, los objetivos de los planes y programas no se realizan por decreto. Es necesaria una capacitación que no se centre solo en proporcionar información a los docentes sobre dichos objetivos, ni que proporcione solo conocimientos teóricos. Hacerlo así se consideraría racionalidad técnica: creer que la aplicación de los conocimientos teóricos son suficientes para resolver problemas dentro de la práctica profesional (Shön, 1987). Los conocimientos teóricos están diseñados para resolver problemas bien definidos y estructurados, pero en la práctica, los problemas se construyen dentro de una zona indeterminada donde los conocimientos son aplicados y se exige de los profesionistas el despliegue de diversas estrategias de solución.

Por otro lado, un constructo que ha cobrado relevancia en la investigación educativa y que aún no ha sido estudiado lo suficiente son los afectos. El afecto es un sistema de representación que permite codificar información significativa del contexto, la cognición y afectos propios y de otros (Gómez-Chacón, 2003). Se ha encontrado que la relación existente entre los afectos y el aprendizaje es cíclico, por ejemplo, la experiencia de aprender matemáticas produce diversas reacciones emocionales e influyen en la formación de las creencias, que a su vez tienen una consecuencia directa en el comportamiento de los alumnos en situaciones de aprendizaje (Nuria. et al. 2005).

Bajo esta argumentación, consideramos que los docentes deben experimentar algunas actividades que les representen un reto, y a partir de enfrentarse a ella, reflexionen sobre sus creencias, sobre las características propias de las actividades, así como los recursos cognitivos y sociales exigidos y los afectos que desencadenan, y a partir de ello se hagan propuestas sobre su futura implementación al nivel acorde al conocimiento de los alumnos.

Método 

Se está realizando una investigación con profesores en activo de diversos niveles que abarcan desde la primaria hasta bachillerato, a quienes se les da capacitación por medio de talleres de actualización docente. En este documento se reporta la primera etapa de la investigación, que consiste en la recopilación de datos de los docentes en capacitación. El objetivo es analizar las reflexiones que hacen de una actividad en términos de exigencias cognitivas, afectivas y sociales, identificando, además, sus creencias sobre la enseñanza y el aprendizaje.

La actividad consistió en una tarea matemática donde se promovió el aprendizaje colaborativo. El estudio es cualitativo, se analizan: producciones escritas de los docentes, opiniones expresadas ante el grupo, anotaciones de los investigadores sobre lo discutido al interior de los equipos y videograbaciones.

Actividad matemática

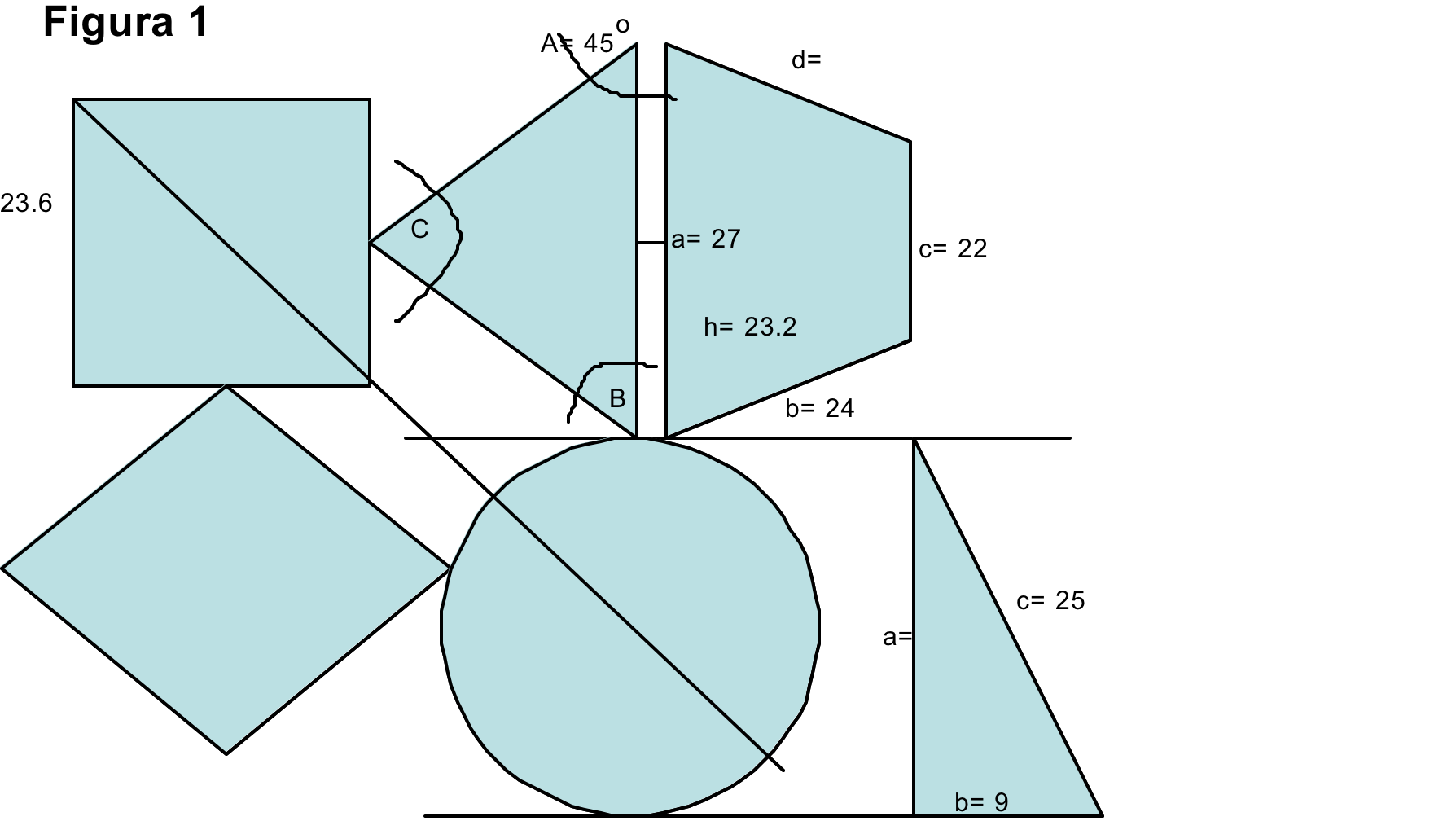
Esta actividad se dividió en dos fases. En la primera, fue elegido un profesor de matemáticas que dirigiera a sus compañeros en la elaboración de una serie de figuras geométricas (figura 1) haciendo uso solo de la palabra. Una vez terminada la actividad, se proyectó la figura para compararse con los dibujos de los maestros. Algunos mostraron su dibujo y expresaron la dificultad que encontraron para realizarlo. En la segunda fase se les presentaron las mismas figuras ahora con valores, y se les pidió que en equipos, donde había un maestro de matemáticas, encontraran los lados marcados con letras de las figuras así como su perímetro y área, además de los ángulos del triángulo equilátero.

Los maestros de matemáticas no debían resolver la actividad, sino proporcionar apoyos necesarios para que el equipo llegara a la solución. Finalmente, algunos profesores de los equipos expresaron las dificultades encontradas, su opinión sobre el apoyo recibido y los afectos que les provocó resolver la actividad. Los profesores de matemáticas por su parte, expresaron las dificultades que percibieron en el equipo, el tipo de apoyo que dieron y los afectos que les provocó la actividad.

Exigencias cognitivas de la actividad matemática

• Para realizar bien el dibujo, la descripción de las figuras geométricas debían hacerse utilizando conceptos matemáticos y éstos deben ser entendidos por los
• En el segundo momento, los maestros debían deducir algunas medidas, apoyándose con las proporcionadas en otras y con ello obtener el perímetro de
• Para obtener el perímetro y el área debían tener claros ambos conceptos, además de tener presentes las fórmulas de las figuras geométricas
• Para obtener los ángulos del triángulo equilátero, tenían que tener presentes sus características. 

Resultados

Reconocemos que el aprendizaje es situado y referido a un contenido (Brown, et al. 1989), y que cada maestro podría haber expresado una concepción diferenciada según la materia a la que se hiciera referencia. Sin embargo se les pidió que expresaran de manera general lo que entendían por enseñanza y aprendizaje antes de llevar a cabo la actividad. De manera general, la concepción que prevaleció fue la de transmitir conocimientos: el maestro debe “transmitir conocimientos a los alumnos que les sirva para aplicarlos en la vida” aunque los maestros de bachillerato reconocieron que no todo el conocimiento “se puede concretizar (ni) todo lo que se aprende en la escuela se puede aplicar en la vida cotidiana” sino que “tiene otras utilidades” en los campos exclusivos de la materia a la que se refiere. Los profesores expresaron que la enseñanza tiene por objetivo que “los alumnos construyan su propio conocimiento, sin la ayuda del maestro” pero en algunos casos como en las materias de ciencias y matemáticas “se deben rescatar los conocimientos previos”, pero, éstos son deficientes y “antes que resolver problemas, es necesario que sepan los procedimientos”.

Si se considera que las creencias son representaciones sobre la información y experiencias adoptadas del mundo y que tienen un gran efecto en las acciones (Hoffer y Pintrich, 1997), se podría deducir que la enseñanza de los profesores se caracteriza por ser tradicional.

Por otro lado, al inicio de la primera fase de la actividad, algunos profesores hicieron expresiones de descontento y rechazo cuando se enteraron que involucraba matemáticas, pero se les animó a no darse por vencidos antes de comenzar. Al finalizar el primer momento, ninguno de los profesores logró hacer su dibujo semejante al que se les proyectó, las reflexiones de los profesores fueron categorizadas en:

1. Desconocimiento de términos utilizados por el profesor de matemáticas: “línea perpendicular”, “vértice” y “trapecio girado a 90 grados”.
2. Dificultad de la A pesar de tratarse de figuras conocidas por todos, se les dificultó ubicarlas espacialmente porque no fueron presentadas en la posición tradicional: “no podía imaginarme un trapecio volteado, porque siempre lo había visto así (de manera horizontal)” lo que provocó que se dejara de poner atención “estuvo muy difícil, me di cuenta de que ya no seguía todas las instrucciones del maestro, solo esperaba que dijera la figura y la dibujaba como fuera, lo importante era terminarlo”.
3. Conocimientos previos de los Fue una sorpresa, incluso para los profesores de matemáticas, darse cuenta de todos los conocimientos que la actividad exigía a los alumnos: “¿todo esto deben saber los alumnos? pobrecitos” y en algunos casos generalizaron sus reflexiones a otras materias “no me había puesto a pensar en todo lo que deben saber los alumnos, en español puede suceder igual cuando vemos el tema de poesía por ejemplo”.
4. Afectos producidos por la Se reconoció el rechazo a la actividad matemática por la creencia de que son difíciles: “desde que dijeron que eran matemáticas me cerré, hice el dibujo nada más porque ustedes pasaban a ver como lo hacíamos”.
5. El método expositivo como recurso de enseñanza. Los maestros compararon esta fase de la actividad con la exposición como único recurso utilizado en “cuando vi la figura pensé que iba a ser fácil dictárselas, pero con las preguntas que me hicieron pensé que no sabían nada y no me iba a detener por eso (…) pero me doy cuenta de que así soy en clase, les digo a los alumnos ‘esto ya lo deberían saber y no me voy a parar para explicarlo de nuevo’ y continúo con el tema”, “la mayoría de los maestros planean sus clases explicando, sin utilizar otras técnicas para que les quede más claro a los alumnos”. 

En la segunda fase de la actividad, los maestros reunidos en equipos buscaron los valores que se les pedían. Nuevamente se expresó rechazo por la actividad pero los maestros que proporcionaban guías los animaron a continuar y encaminaban la respuesta para que fuera completada por los demás. Finalmente, todos los equipos llegaron a la solución y sus reflexiones con respecto a la dificultad de la tarea y los conocimientos previos de los alumnos, fueron en el mismo sentido de los mencionados anteriormente. Pero en los afectos producidos por la actividad se reconoció la inestabilidad e intensidad de las respuestas afectivas (McLeod, 1992). Fue reconocido que conforme los maestros se percibían eficaces en la solución de la tarea su respuesta de rechazo inicial fue sustituida paulatinamente por la satisfacción: “al principio no entendía nada y me desesperé cuando mis compañeros entendían el ejercicio, pero el maestro se dio cuenta y me comenzó a explicar poco a poco (…) cuando le entendí me emocioné y el tiempo se me pasó rápido”.

En esta fase los docentes de matemáticas valoraron el aprendizaje colaborativo y lo contemplaron como una opción para llevarlo a sus clases: “pedimos a los alumnos que hagan las cosas solos porque pensamos que así deben aprender, pero me di cuenta que mientras yo explicaba a una maestra, otro que ya había entendido, explicaba a los demás, además me di cuenta de los errores que tienen y así les pude ayudar mejor (…) me convenció este tipo de trabajo para hacerlo con mis alumnos”.

Conclusiones

Planear situaciones de aprendizaje, a partir de los obstáculos que encuentran los alumnos, es una de las competencias que requiere el docente para la enseñanza. Pero para conocer a fondo los posibles problemas que obstaculizan el aprendizaje se propuso que los profesores se enfrentaran a la actividad con el fin de que experimentaran sus exigencias y los recursos que se deben poner en juego para hacerle frente. A partir de ello, durante sus reflexiones, los profesores reconocieron la necesidad de analizar las características de la actividad, los recursos cognitivos y sociales que demandaba así como las respuestas afectivas que provocaba.

Entre los recursos cognitivos expresados se encontraron los conocimientos previos y manejo de conceptos de la materia a la que se refiere, que en muchos casos se da por sentado que se dominan.

Un aspecto que no había sido tomado en cuenta por los profesores fue las respuestas afectivas provocadas por la actividad. Éstas se presentan con cierta intensidad inicial, pero son proclives a variar a lo largo de la actividad debido a su inestabilidad. En este sentido, es necesario aclarar que las respuestas afectivas iniciales reconocidas fueron el rechazo y disgusto, no se mencionaron respuestas afectivas positivas, pero se reconoció que el rechazo fue sustituido por la satisfacción cuando los miembros de los equipos se sintieron apoyados en el proceso de solución, lo que les permitió percibirse eficaces, de esta forma se evidenció las bondades del aprendizaje colaborativo y las habilidades sociales que se despliegan (negociación, argumentación de propuestas, prueba de varias soluciones, toma de acuerdos).

Bibliografía 

• Brown, J., Collins, A., & Duguid, P. (1989) Situated cognition and the culture of learning.
• Educational Researcher. January- February, pp 32-42.
• Gómez- Chacón, I. (2003) La tarea intelectual en matemáticas afecto, meta-afecto, y los sistemas de creencias. Boletín de la Asociación Matemática Venezolana. 10(2), pp 225-247.
• Hofer, B., y Pintrich, P. (1997) The development of epistemological theories: Beliefs about knowledge and knowing and their relation to learning. En Review of Educational Research. 67 (1), pp 88-140.
• McLeod, D. (1992). Research on affect in mathematics education: A reconceptualization. En Douglas A. Grows (ed.), Handbook of Research on Mathematics Teaching and Learning, Macmillian, NCTM New York, pp. 575-596.
• Nuria, G., Blanco, L., y Guerrero, E. (2005) El dominio afectivo en el aprendizaje de las matemáticas. Una revisión de sus descriptores básicos. Revista Ibero Americana de Educación Matemática. No. 2, pp 15-32.
• Perrenoud, P. (2004) Diez nuevas competencias para enseñar. Barcelona: Graó. Colección Biblioteca del Aula, No. 196.
• Putnam, R. (1992). Teaching the ‘hows’ of mathematics for everyday life: A case study of a fifthgrade teacher. Elementary School Journal, 93(2), 163-177.
• SEP (2005) Primer diálogo con Directores Escolares. Memoria. Subsecretaría de Educación Básica. Dirección General de Desarrollo Curricular.
• Shön, D. (1987). La formación de profesionales reflexivos. Hacia un nuevo diseño de la enseñanza y el aprendizaje en las profesiones. Temas de educación Paidós.